What is your school’s multiplication fact recall data telling you? Is now a good time to review your actual teaching of instant recall of multiplication facts? I say ‘actual teaching’ because whilst creating practice time with high engagement in pure recall practice is vital, it is by no means the guarantee of securing such recall across the school and by the ages expected. To do that requires a much more thorough whole school approach that has a wider pedagogical story, driven by the prequels (conceptual understanding of the sequence of multiples) and cemented by the sequels (application of factual recall).
Here we take any given multiplication table (for example, the x3 multiplication table) and we explore the 5-stage process of teaching the instant recall of facts. The factual recall itself occurs at Stage 3, but only after the prequels of Stages 1 and 2, and immediately consolidated by the sequels of Stages 4 and 5.
Stage 1: seeing and counting the multiples
The first stage is to engage the learner with the structured counting of the multiples. This starts off by leaning on the child’s ability to simply count objects, ‘1,2,3,4,5,6,7,8,9…’etc. but here layered alongside strong imagery and with the out-loud counting deliberately over-emphasising the group totals/multiples; ‘1,2,3…4,5,6…7,8,9…’etc.
A variation of imagery is useful, as is a simultaneous progression of gradually more abstract imagery, alongside a gradual withdrawing of the over-emphasised counting in ones…
…until it is just the sequence of the first 10 multiples that the child is seeing and reading.
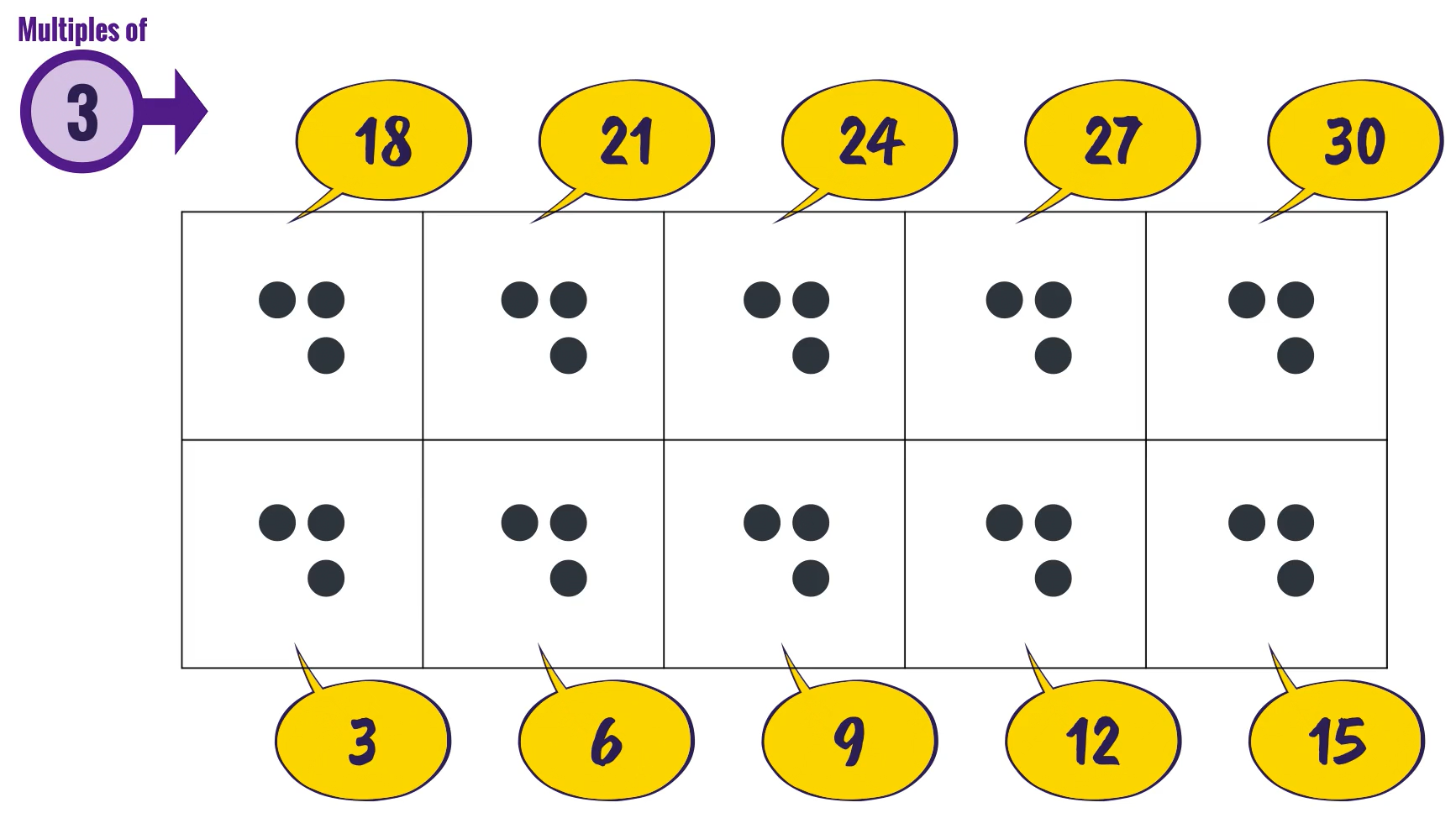
Stage 2: reciting the multiples and knowing their positions
The second stage builds on the first stage of ‘seeing’ the arrangements of the amounts. Now our focus is on the learner reciting the sequence of the first 5 multiples (‘3,6,9,12,15’).
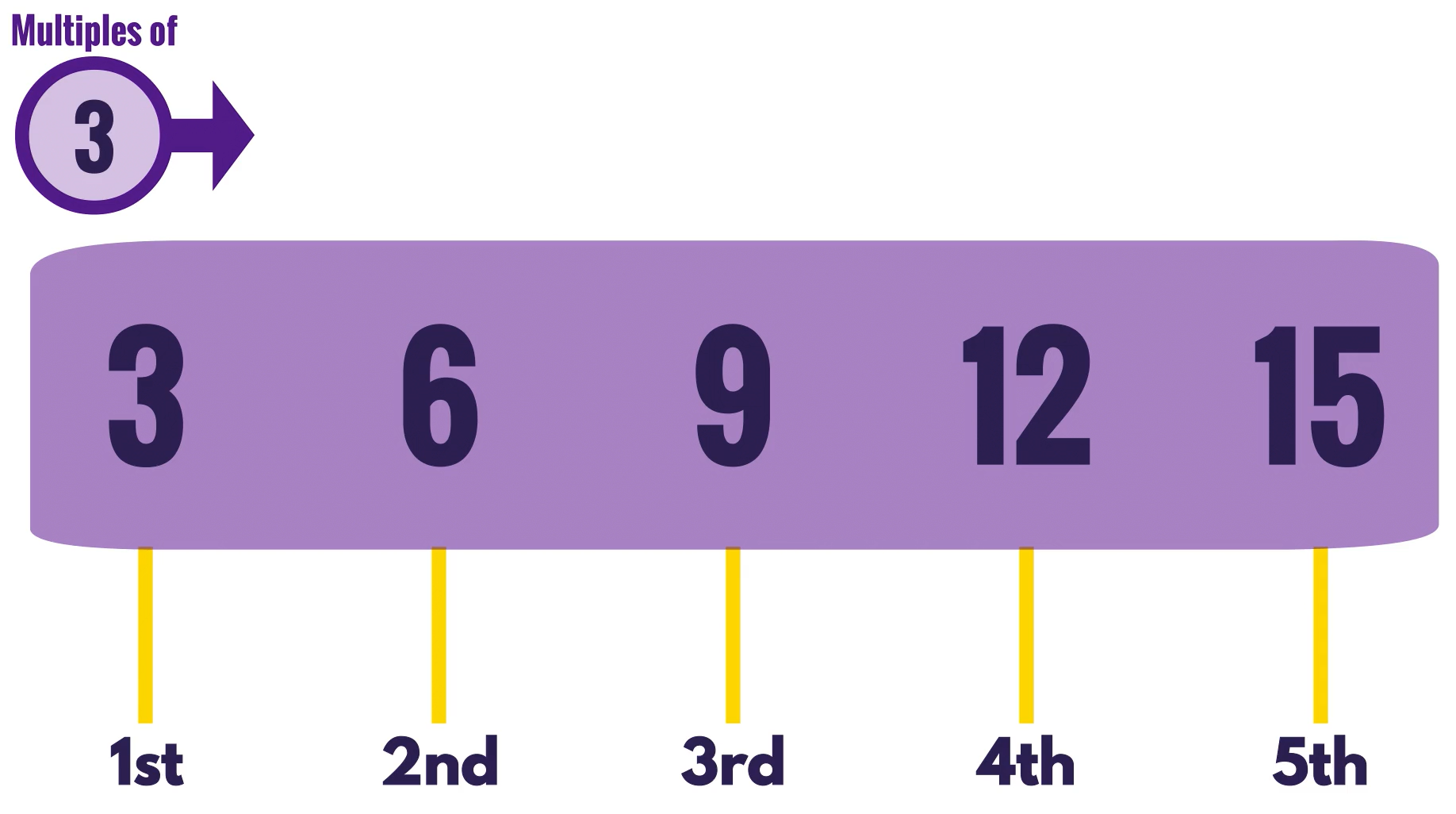
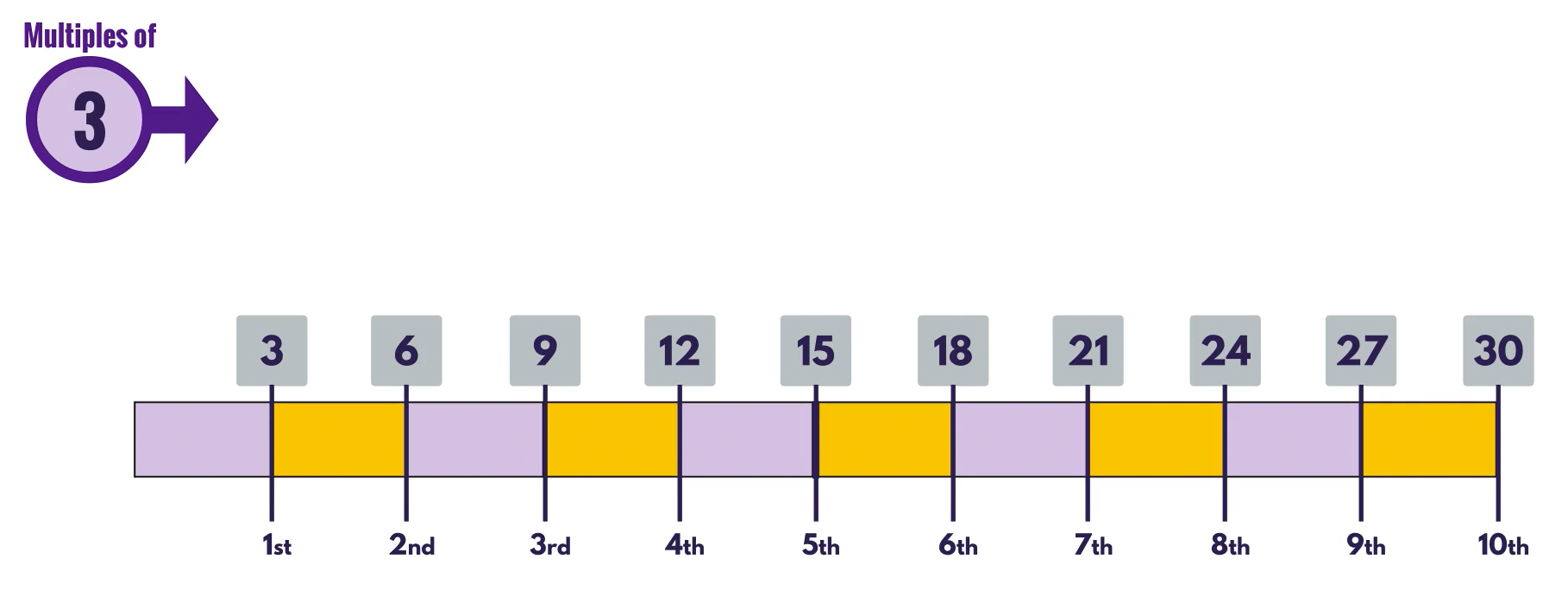
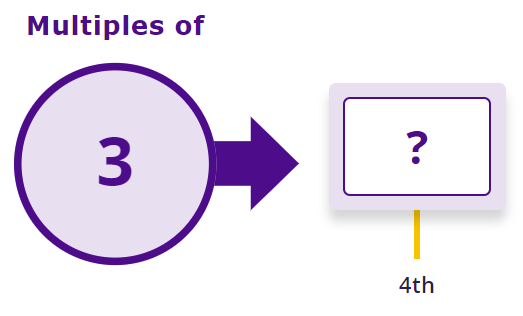
Then, increasing their fluency with this pattern to the point where they know the position of each multiple out of sequence (‘What is the 4th multiple of 3?).
The same process is then repeated with the next 5 multiples (‘18,21,24,27,30’).
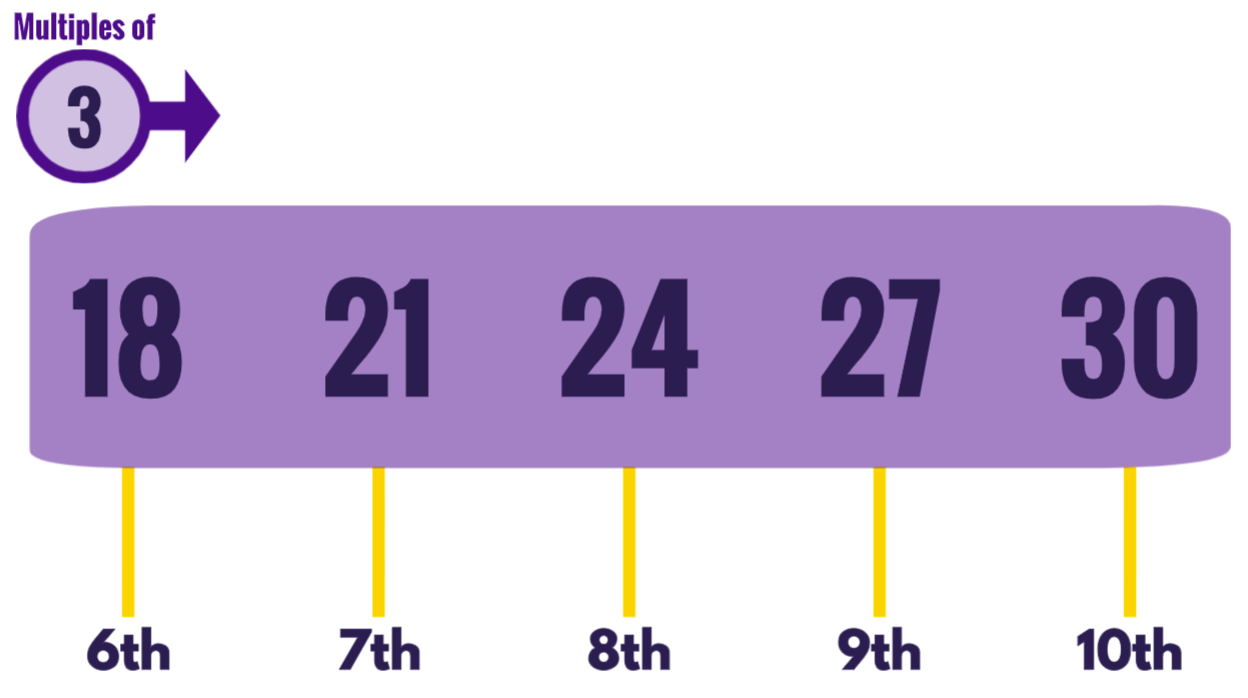
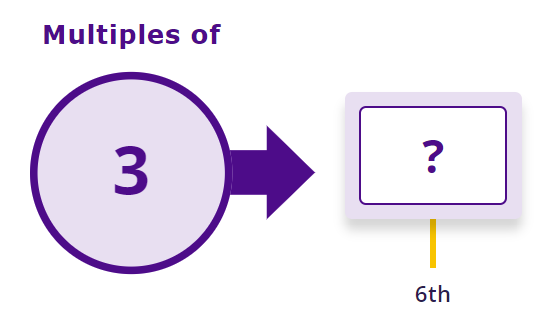
This brings us to the point where the child is able to tell us the correct multiple when given the position (from the 1st to the 10th multiple).
This is also the stage to bring in any connections to ‘other tables’ (i.e., previous multiplication table fact recall), being careful not to overcook this teaching idea as its usefulness to recall development can easily be overstated.
Stage 3: recalling multiplication facts as facts
On entering this stage, children should ‘see’ the actual table organised as a list of facts, with the idea of factual recall (knowing the ‘answer’ as well as they know their own name, with zero thinking time) being re-explained, reiterated and modelled.

When children arrive at this recall stage with the conceptual understanding from Stage 1, and with knowledge of the position of the multiples from Stage 2, this becomes a far shorter and more comfortable process. Although learners need a degree of development space here, any child that is far from instant recall should be taken back to Stage 1 or 2 as appropriate. Again, we should be careful to increase the recall demand incrementally, and at a pace that suits the learner. For example, narrowing the recall session to a mix of 2×3,3×3,4×3,5×3 before moving on to a mix of 3×2,3×3,4×3,5×3 etc.
Be careful not to let children move on from this stage until their recall is such that they use virtually no thinking time to recall the fact. Questions at this stage involve just the two commutative multiplication facts (3×4, 4×3), only progressing to division facts at the next stage once they have ‘red hot’ recall from this stage.
Stage 4: recalling and using division facts
With secure recall of commutative facts now behind us and having previously taught the ideas behind ‘turning multiplication facts into division facts’, we can now combine these two pieces of number knowledge. So, children can now be given any multiplication fact from the table and can instantly turn that 1 fact into 4 facts, writing all 4 equations out quickly, and reading all 4 equations articulately.
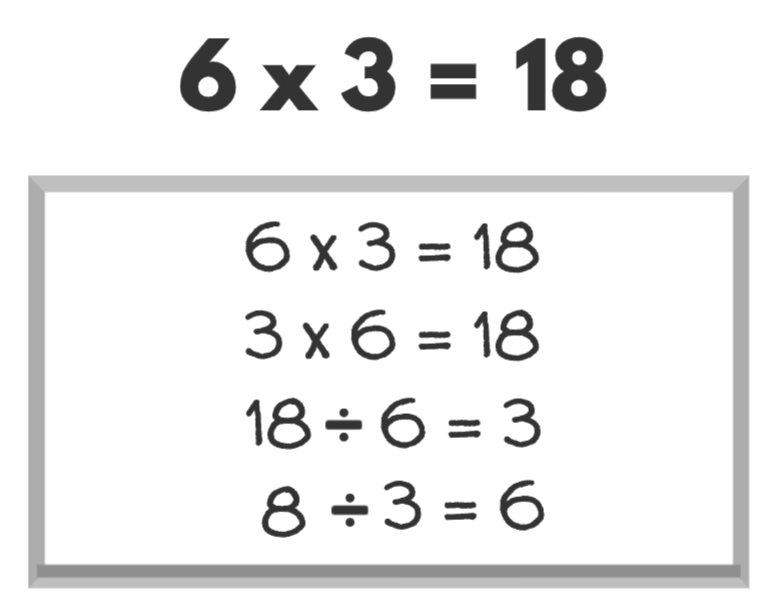
However, there is something more to be gained here. Since children are now so familiar with the sequence of multiples from Stage 2, we can give them any whole number up to the 10th multiple and ask them to tell us the highest multiple that can be seen within that number.
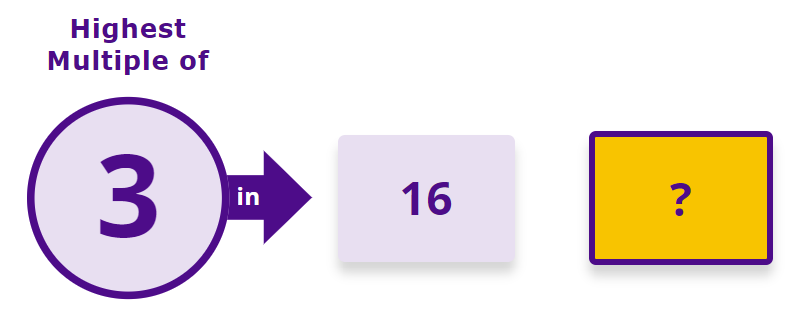
This should progress until the child is also telling us which multiple this is, in terms of its position in the sequence (the 1st, 2nd, 3rd etc.).
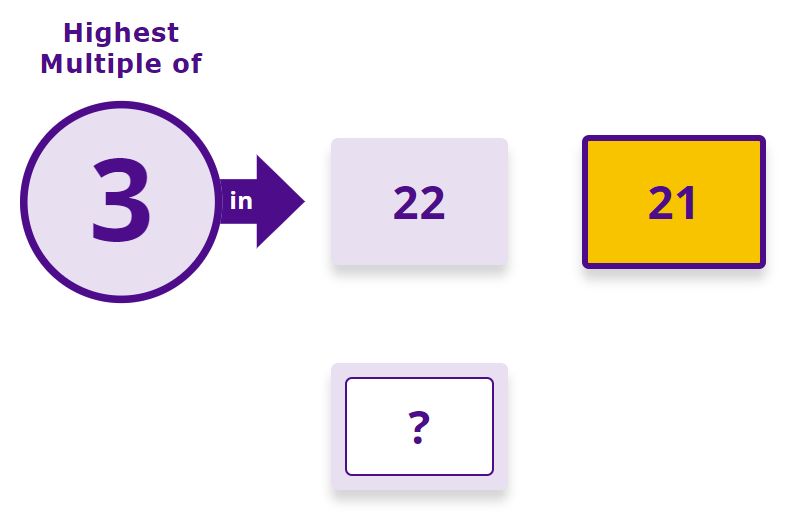
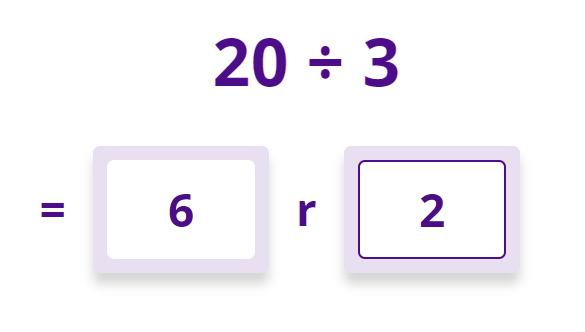
Then, progressing further, so the child is now telling us how many are ‘left over’ as well.
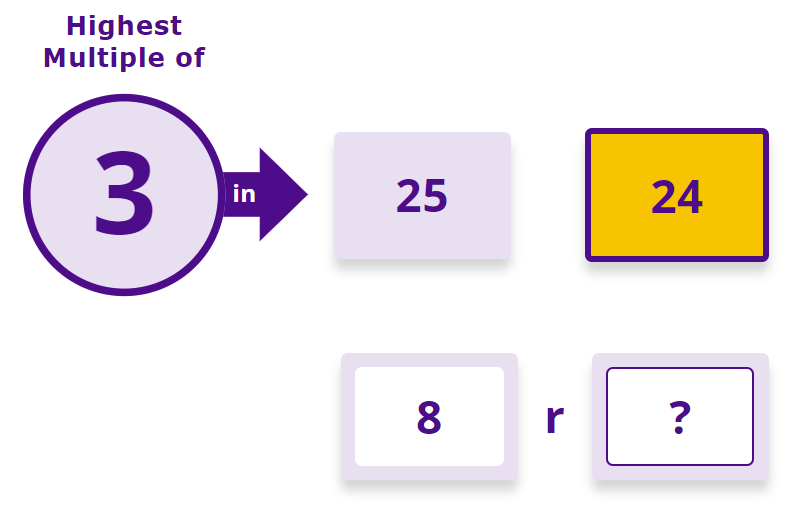
This is a simple fun activity with high success due to all pre-requisite background knowledge already being in place. It is also a highly effective activity since it retrieves the idea of the positions of the multiples, strengthening this further now we are the other side of the factual recall stage. You can also see that the child is already completing ‘division with remainders’ in that they are identifying the highest multiple, using that to know how many groups can be found within the starting pile and identifying the remainder. All we need to do now is to re-explain this connection as division, and re-position the ‘question’ as a division question.
Stage 5: retrieval and transfer
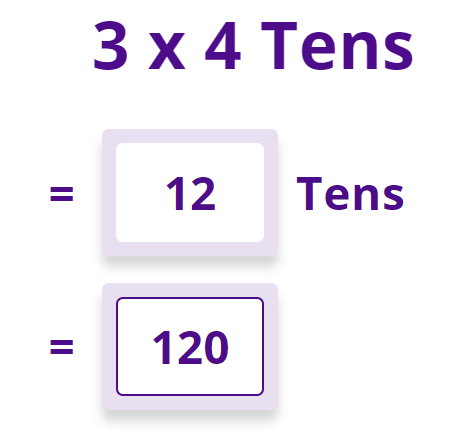
Although all 5 stages are vital for smooth progression across the school, perhaps the most undervalued stage is this one where the teacher takes the recently secured multiplication fact recall and retrieves it in the progressive contexts of everyday objects, tens, multiples of ten and then simple 1-digit x 2-digit calculations. This can’t be ad-hoc. We are talking of a strategic and systematic approach across the school that ensures all learners come back to recently secured facts and transfer them into the context of tens. If 3 x 4 = 12 is instantly recalled as a fact, 3 x 40 = 120 is brought into the same place, with the same thinking time required (i.e. virtually none).


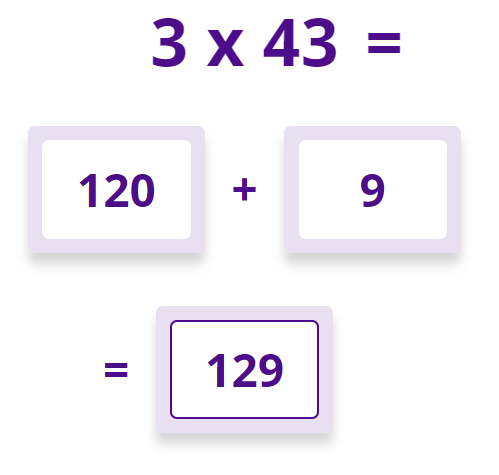
This retrieval and transfer approach is the ultimate win-win for teachers of number; strengthening recent learning and simultaneously expanding the child’s number knowledge with no extra effort. The retrieval and transfer journey should continue to systematically build and expand from there, through a well-thought-out number programme (eg multiplying by 3-digit whole numbers, decimals etc.). Of particular importance is that children learn to use these facts for quick mental 1-digt multiplied by 2-digit calculations with only a small increase in thinking time from the 3×4 moments and 3×40 moments mentioned above.
Leadership Takeaways
Overall, we can see the key lines of progression within each stage, and summarised these in the table below.
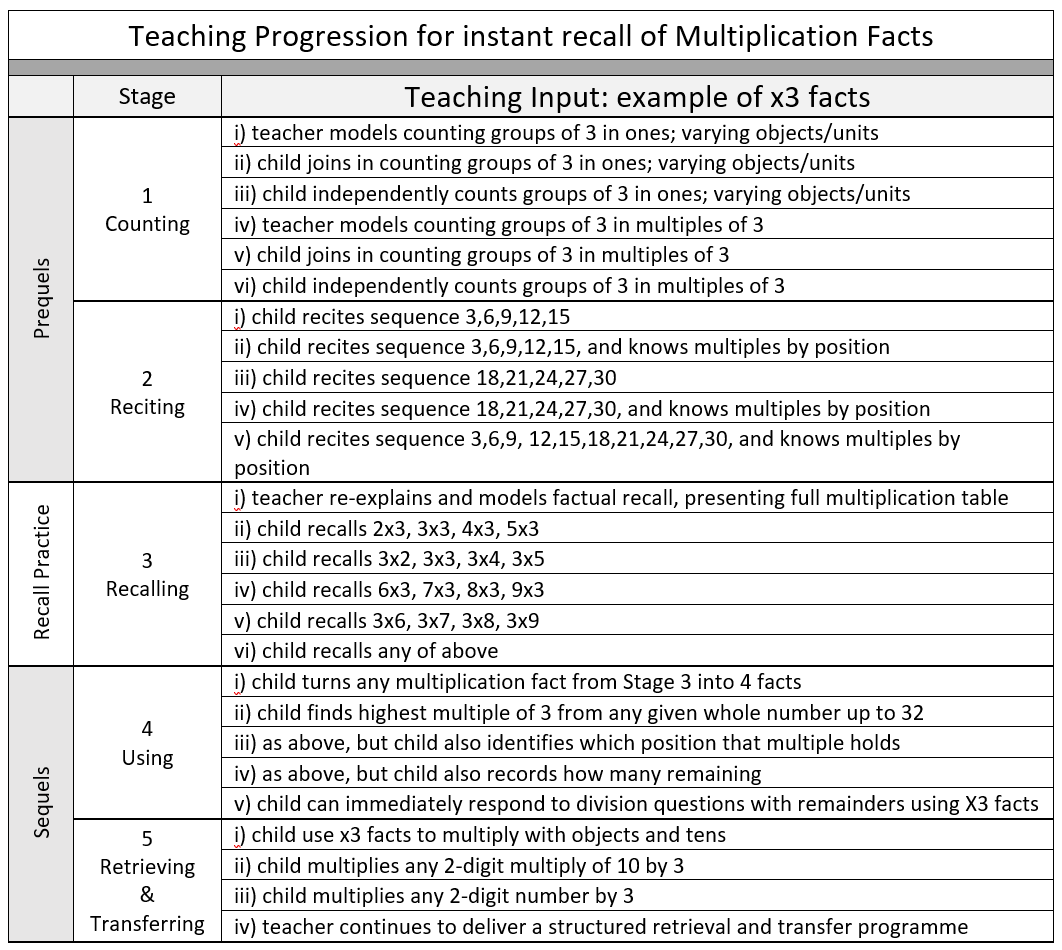
Seeing this level of pedagogical structure allows us to identify some obvious implications for a whole-school approach to teaching multiplication fact recall:
- Emphasis on stages 1,2 and 4,5: quite often the approach is to thump away at recall of facts found at Stage 3. However, and somewhat counterintuitively, the real gains are made outside of this practice. It is the prequels and sequels that have the most direct impact on recall.
- Resources to support this level of teaching/thoroughness: clearly, to deliver this vision across a school without increasing workload requires a full Edtech solution. This is more than providing on online space to practice. This is about having a learning platform that supports this level of pedagogy alongside workload reduction.
- Intervention: the 5 stages can be used as a simple model to ensure all children are on a progressive path to improved recall, moving them back if you find that they are at a stage they are not cognitively prepared for. Note the highly inclusive start to the path for each multiplication table, requiring the ability to count in ones only means all children who can count can start on that path. We have all seen learners taken straight to Stages 2 or 3 without this crucial and easy kick-start imagery.
- Prevention 1, Continuity across year groups: Of course, prevention is better than cure/intervention and here are three simple considerations, starting with the need to build the larger progression into a whole-school approach. We can see that securing the recall of each table is a process and not an event, and quite often the process isn’t confined to one year group but slices across the summer holiday/year group transition.
- Prevention 2, Transparent accountability: Linked to this is the need to have a whole-school solution that tracks all children, across all 5 stages, across all multiplication tables. Again, this is where the right pedagogically based learning platform can do literally all of the work for you, leaving you with the just the view of the red flags to respond to (if any were to wave).
- Prevention 3, Focus on the vulnerable group: The scrutiny of the waving red flags, and that ‘in-classroom’ response, needs to be highly focused on that group of children who are most vulnerable to not securing this recall. Be very wary of the seemingly impressive whole-class verbal demonstration of recall, where the vulnerable group are often masked by the volume and confidence of the non-vulnerable group.









