We teach children how to solve problems in Maths, both for the sake of problem solving in Maths but also as a context for learning real-life problem solving. It’s ironic, then, we are still unable to solve our own BIG PROBLEM; how to guarantee all children become truly fluent processing number…before they are 10-years old.
In England, for example, we already know that 1 in 4 children are likely to leave school this year with insufficient mathematical knowledge. That, right there, is the actual ‘expected standard’. Even then, many of the 3 in 4 children that do hit the ‘expected standard’ will have spent months, if not years, receiving ‘intervention’. Urgent academic rescue has also become the ‘expected standard’. Anyone who thinks primary maths is now under control needs an ‘emperor’s clothes’ moment. The top-line statistics tell us we do not have control of children’s primary maths learning journeys.
The path out of these dark woods isn’t found by moving more deeply in. Indeed, it is the obsession with ‘deeper’ that is the problem. Schools have found themselves in this darkness via the agenda for more problem-solving, more reasoning and more ‘mastery’. The thinking goes something like this, ‘Maths is all about problem-solving, so let’s learn all of Maths through solving problems’. Superficially, this makes sense. However, children must first be genuinely fluent processing number, to then create the cognitive capacity needed to focus attention on the problem to solve. Just as children need to learn to read so they can read to learn, the ‘means’ is not the same as the ‘end’. Mathematics is the ‘end’, but Number-Fluency is the ‘means’ (see Peps Macca’s writing here for a more thorough explanation of how the educational ‘means’ and ‘end’ need to be viewed separately).
So, within primary mathematics there is a central domain of essential number-fluency that needs top priority and can be represented like so.
Solving ‘the Maths problem’ starts by having control over every child’s essential number-fluency learning journey.
I’ve worked face-to-face with literally thousands of teachers on their teaching of number-fluency, and I’m often asked what the top priority is within this domain. My response, over 20 years of consultancy, has remained the same. Children must win the instant recall of all 1-digit + 1-digit addition facts whilst they are still 7-years old. There is a bizarre paradox taking place out there; the Addition Fact Recall Learning Journey is the most important academic role a primary school holds (matched in importance only by phonics), yet, typically, is the learning journey that schools exhibit the least success and confidence with. So, here are my 8 rules to follow (or use as a check-list) when starting out gaining control of your children’s primary maths learning journeys.
Addition Fact Recall: 8 Rules to Follow
- Teach the idea of recall (if this, then that)
Rule 1 is to teach the child what we mean by recall. As teachers we know what instant recall looks like (although, interestingly, when I first started off training teachers in Number-Fluency, the idea of recall needed a thorough articulation). This first rule is agreeing what we mean by recall with the young child starting off on their number fact learning journey. If the child can respond immediately to a picture of a dog, a ball, ‘what’s your name?’ etc., without needing to stop and think/process, we not only have a recall foundation to connect further information to, but we can also speak about the concept of recall with the child. Inviting them to notice what happened, i.e. the sensation of ‘no thinking time’, therefore allowing us, as teachers, to develop the metacognitive benefit of strengthening the centrepiece of this ‘instant recall schema’.

When the child learns the idea of recall, early number facts are added to the schema and are not floating around as isolated pieces of information to recall, thus accelerating the acquisition of new facts into the memory (short-term and long-term). It might be useful to think of what it looks like when a child hasn’t yet ‘got the idea’. When a 7-year old child is asked to respond to ‘6+7’ and they place one number in their head and count on, or shuffle a part of one number across to make 10 and then add on the remaining part, the responsive teaching point isn’t about 6+7, and it isn’t even, ‘Learn it as a fact next time please’, but rather it can be paraphrased as, ‘Notice how your thinking went ‘thought-thought-thought’, let me show you how you can already think with one thought for a picture of a dog, now also use one thought for this’. The very top-level concept here is, ‘see this, say that’. Regardless of understanding the fact (for now), the child must apply the idea that when they see x they respond with y, just as they do in phonics programmes when connecting letters and sounds.
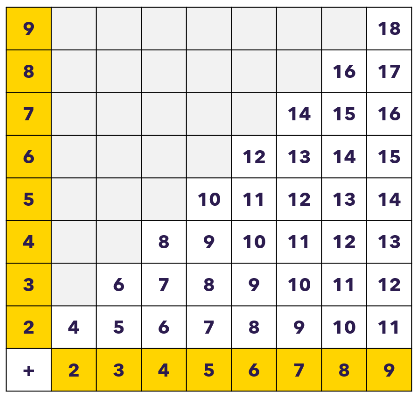
- Know the content you’re dealing with (36 Facts)
Rule 2 is to clarify across the school which isolated pieces of recall we are going to secure with every child. For me, this boils down to 36 essential pieces of information, including all 1-digit + 1-digit facts, ranging from 2+2 to 9+9. Note, I don’t include +1 facts (such as 6+1) since adding one is a concept and procedure taught outside of this learning, as an extension to knowing the next number name as we verbally count. I also don’t include the commutative version of each fact. Again, the commutive law is taught as an isolated concept outside of this learning, and leads children to understand that recalling, for example, 5 + 7 = 12, means they also have the recall of 7 + 5 = 12.
- Breakdown the entire content (10 Small-Steps)
Now we know what we’re dealing with, we start to systemise the learning journey. This involves breaking down the entire Addition Fact Recall Learning Journey into smaller cognitively-manageable steps. I have scrutinised many different versions of this breakdown and worked over many years on perfecting my own. Now, when combining all this thinking, I am left with these 10 simple steps:
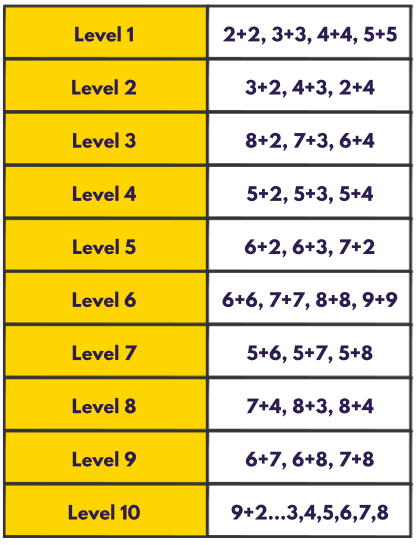
Step 1 – these facts arise out of the ‘finger doubles’ that children experience through finger rhymes/song/actions.
Step 2 – the remaining addition facts where both numbers being added are less than 5.
Step 3 – number bonds to 10; classic, timeless, essential, mathematical building blocks. Love!
Step 4 – all start with 5, adding 2, 3, 4…introduced by connecting the commonality of ‘5 add something’ on a 10-frame.
Step 5 – the remaining facts that total less than 10. Notice how Steps 1 to 5 don’t reach beyond 10 (and so can be addressed by children working at this level), and Steps 6 to 10 do.
Step 6 – the remaining single-digit doubles.
Step 7 – all start with 5, adding 6, 7, 8…introduced by connecting the commonality of ‘5 add something’ on two 10-frames.
Step 8 – introduced by extending the idea from the previous step of making 10 on two 10-frames and feeling/seeing the remaining amount (totals of 11 and 12 only).
Step 9 – as above, making 10 on two 10-frames and feeling/seeing the remaining amount (this time with totals of 13, 14, 15).
Step 10 – these facts all start with 9, and so there is a single idea being taught, i.e. to see ‘one’ from the other number being used to ‘finish off making 10’.
- Use transparent tracking (which step and when)
Before we go further into generating the recall, it’s essential to map the 10 small-steps (or however many steps you choose) into an age-related expected journey. The overarching timescales used should lead children to finish the journey halfway through the school year they turn 7-years, whilst leaving sufficient time between each smaller step to shift the recall from the child’s short-term memory into the long-term. At a school-leadership level, the information this exercise of ‘mapping against time’ produces, is vital to success. Only once we have agreed when each small step of recall will be secured in the child’s mind, do we start to gain control of the learning journey. Put it another way, when schools can’t see, or don’t regularly look at, the proportion of children on-track, control of this crucial journey is lost. Alternatively, as soon as we have the simple view of which children have the recall that we expect them to have at any point in time, we have control! Even if there are only 30% of children hitting the recall standard, that gives a teacher two attainable short-term targets at the next check in time-stamp; i) maintain that same 30%, and, ii) increase that proportion by targeting those next few children who are closest to becoming ‘on-track’. This means the proportion of children ‘on-track’ is always on the rise, as well as being more relaxing for the class-teacher who isn’t then expected to fix a whole-school problem on their own, overnight! From a whole-school vista, it means more teachers, more often, are hitting more precise next steps for recall, with more children, through their face-to-face daily input; again, vital for long-term whole-school mathematics success.
- Breakdown each small step (1 Recall Goal)
Once we do arrive at the point of teaching each small step of recall, we can get inside each small step and move into the heart of teaching the recall. There is a huge difference between teaching number-fact recall and simply providing a space for children to practise recall. Teaching recall necessitates a much broader sequence of learning than mere flashcard recognition, and that is why Rule 8 is indeed a rule! For now, let us consider that each small step has, typically, 3 or 4 new facts for children to start recalling instantly, and that we can break that down further by introducing one new fact at a time. In other words, we are moving from a ‘small-step’ to the smallest step! It is always useful to start with the child recalling factual content already in their long-term memory. That means we can start at the previous small-step, and, from there, introduce a single fact from the new small-step, integrating it into the secure recall from the known facts with a flashcard-learning approach. For example, using the 10 small-steps above, the child learning Step 8 might have flashcard learning that moves from rotating ‘5+6’ and ‘5+7’ to then include ‘7+4’ for the first time. This technique frees up all the child’s available cognitive space to focus attention on the new fact. Once that new fact has started to hit the criteria of ‘instant recall’, we can drop one of the facts from the previous small-step and introduce another fact from the current small-step. For example, now rotating 3 flashcards of ‘5+6’, ‘7+4’ and ‘8+3’. Eventually, we will be rotating just the new facts from this current small-step. Each time a new fact is injected into the flashcard rotation, the teacher introduces the fact by briefly coming back to the imagery of the number relationship involved (again, see Rule 8) and modelling the instant recall, paraphrasing the ‘one-thought’ idea through their out-loud thinking, and being ready to support the child by kindly providing the ‘answer’ if the child’s response to the flashcard is too hesitant or if their processing is beginning to move into a ‘thought-thought’ mode.
- Systemise little and often (only use EdTech)
Of course, the above description of rotating flashcards is fine and dandy for those teaching a child one-to-one. In the real world, class teachers can’t hit this simple ‘flashcard rotation’ without immediately becoming ethically frustrated that some children already have recall beyond their face-to-face input, whilst other children aren’t ready for the input. This is the crux of the problem, too many children turn up to school and their teacher – through no fault of their own – isn’t pushing that child’s buttons regarding next steps for recall. When that happens across a class of children, across a week, term, year… everything quickly falls apart! This is one of the curriculum places where EdTech is essential. Unfortunately, schools came through the EdTech front door feeling obliged to use software because it existed and was the future. We now see huge educational software investments from global tech companies confusing the EdTech market, not just in terms of whether the glitzy graphics are disguising a paucity of pedagogical thought, but also in terms of which curricula domains needEdTech and which don’t. The primary mathematics number-fact recall journey needs Edtech. Without it, the class teacher simply can’t provide the personalised input and engagement necessary for efficient success. Another thing the class teacher can’t provide is input every evening and weekend, yet the child needs this ‘little and often’, including a caring degree of time pressure for each one-thought response. The old-fashioned number-fact worksheet for homework, and independent learning in school, is intrinsically self-defeating. It provides too much thinking time – opening the door to too many thoughts – and is not personalised enough, or, if the child is immediately firing back ‘answers’ on their sheet, it isn’t worth the photocopying/printing distributing/collecting costs (financial and time). Undoubtedly, the most successful model we have is Bruno Reddy’s TTRS. It’s huge, and globally-growing, success is well warranted given his early vision and execution on all of the above.
- Physically watch the recall (don’t use EdTech)
At the same time as EdTech being essential, this journey is simply too important to completely hand over to software. One of the gaps that arises in the system is when too much reliance is placed on learning platform data and is not triangulated with the teacher’s ongoing judgements and responses to the key self-evaluation question; ‘Is the overall number-fact recall provision (face-to-face and EdTech) genuinely generating the recall that we expect on our mapped out, age/time-related, expected journey?’. The only way to be certain is to observe the child give that immediate response. The recall we require must be observable, repeatedly accurate, and demonstrated over a wide time scale.
A time-efficient ‘daily watch’ and ‘weekly watch’ that includes children demonstrating successful recall at the previous two small-steps, before then showing increasing accuracy at the current small-step, is the perfect blend. It allows the teacher to screen the recall that we are assuming is secure (i.e. the previous two small-steps), thus providing a vital safety-net to spot any recall gaps behind us in the journey. It also gives retrieval time to constantly pull back recently secured recall, strengthening it and embedding it further into the long-term memory. We can also check that recall at the current step is constantly on the up, with the teacher writing in situ ‘mental post-its’ to prompt finding those ‘at risk’ (in terms of number-fact recall) children later in the day for an additional face-to-face input. Almost nothing takes academic priority. For anyone looking for a ready-made daily watch and weekly watch system you can head to these free YouTube resources linked to the 10 small-steps above:
Daily Watch: https://www.youtube.com/playlist?list=PLm28z3XkK8VjBRMk-gfoBY-F77mYQFw6x
Weekly Watch: https://youtu.be/dW04eL8cH1s
- Build broader teaching around the Small Steps (use Prequels and Sequels)
Up to this point we have been thinking of hitting our recall goals through, what we could call, a ‘flashcard learning’ approach; so, we offer up ‘6+7’ (verbally or visually) and the child immediately responds (verbally or in written form) with ‘13’. Rule 8 now peels back all of this to clarify that the flashcard learning moment, whilst it remains the main event, is only part of a sequence of teaching points that build recall. We also need to consider the build up to the main event, i.e. the prequel.
This involves the child initially experiencing the number relationships physically, both indirectly, by watching an adult model with out-loud thinking, and then directly by counting out the number relationships for themselves. This counting out has its own progression involving songs/rhymes/actions (where appropriate), counting on fingers, with play-objects, with blocks, counters on a 10-frame and, ultimately by bouncing along a number line. Gradually, the physical experience is dialled down with the visual experience taking on greater prominence (NB the physical experience was really aimed at taking the visual experience to a deeper level, so it wouldn’t be right to say the visual is now dialled up). Once a child is counting visually, we can expect to see small nods in their mind as they count on from one amount to another, again using number lines, 10-frames etc until the visual aid is completely phased out and the child is mentally counting to find the totals.
Further points to note here:
- there is a sequence of learning experiences happening over time, so it isn’t so much that we have ‘aprequel’ to the main event, but that there are a range of progressive ‘prequels’ to the main event.
- ideally, the child exits the ‘prequels’ stage with the number fact already in their short-term memory. Their subconscious thinking should be along the lines of, ‘Why am I being asked to count this out when I already know what the total is going to be?’. This is the natural way to learn number-fact recall, when the understanding behind the number fact relationship is so well internalised, the flashcard learning at the main event is only being tasked with moving the recall to the long-term memory, as opposed to being the introduction of that recall.
- as we move the child to the flashcard learning, we must handle carefully the transition from counting to not-counting. This progression needs to be made explicit to the learner, giving the child the metacognitive ability to realise (and, ideally, explain back to us) that they used to count out these totals, but now, with recall, they don’t need to. The subconscious thoughts at ‘b’ above, now become conscious. This connects back to Rule 1. We can see why this could be confusing to a young child. We have been saying ‘count out these number relationships’, and now we are saying ‘do not count out these number relationships’! Part of handling this transition to ‘not-counting’ involves not allowing the child to return to counting.
Let’s now move on to coming out of the flashcard learning phase. The main event is over and we are really seeing impressive, quick, one-thought recall from the child. So, now, we must include that fact in a system of daily retrieval practice, using EdTech and not using EdTech (see Rules 6 and 7). From there, we should also move on further to a range of crucial teaching points that we can term ‘sequels’. This is where we strengthen the child’s recall even further by shifting the child’s recall into slightly different number-fluency contexts. Mostly, these ‘retrieval and transfer’ contexts will be using ideas and procedures that have already been made fluent, transferring the recall into familiar contexts those facts haven’t yet been used in. This provides a very clear number-fluency win-win! We strengthen the recall… and the context! As a quick example, if we have recently secured the recall of ‘7 + 8 = 15’ for the child, we can expect our learner to now effortlessly apply this to: 8 + 7, 15 – 7, 15 – 8, 67 + 8 and 70 + 80, since those ideas and procedures have already been made fluent earlier in our learning journey. Indeed, this sets the scene for a school to have a wider curriculum (adopted or created) that has been meticulously constructed, interconnecting simultaneous learning journeys for addition-fact recall and addition calculation progression.
If anyone ever wants to get serious about solving the Maths problem in their home, their class, their school, their group of schools, or even their country, they have to start by working through this early piece of the puzzle. Nearly always, we see ‘the fix’ happening at a stage too far up the kinetic chain. We might try to solve the maths problem at the level of national secondary school Mathematics results, multiplication-fact recall for 9-year-olds, addressing teaching shortages, addressing teacher subject-knowledge, challenging parents’ maths mindsets, more problem-solving for primary aged-children etc. etc. However, without systemising the simplicity of ensuring all children learn to count objects, apply that counting into 1-digit + 1-digit number relationships, transforming that counting into the ‘not-counting’ of instant recall, and only then progressing into wonderful world of retrieval and transfer (the ‘sequels’), any mathematical success is still not being built on a strong foundation.
The teaching of Number-fluency can be turned into a system, a structure, a programme (akin to phonics). Notice the language, ‘…if we have recently secured the recall of ‘7 + 8 = 15’ for the child…’. Number-fluency isn’t something we wait to see if child picks up. It is something we give them, via a strong teaching process that we apply/implement to them. Not all mathematical knowledge will be acquired in this way. So, again, we see the need to distinguish between wider/deeper mathematical knowledge and essential number-fluency. Without this simple differentiated vision of primary maths, and the implications for switching modes of teaching, we will never solve the one maths problem we must solve.









